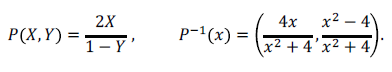Sabemos que los números reales tienen una infinidad de elementos, los cuales pueden ordenarse de mayor a menor; sin embargo, no es posible encontrar al mayor de estos, ya que, si algún número se autoproclama con esta distinción, el elemento n+1 bien haría en contradecir al elemento n ya que él es mayor por una unidad. Esta historia estaría destinada a repetirse por siempre, ello llevo a la necesidad de crear al infinito positivo (∞) , el cual es mayor que cualquier número real pero no pertenece a los reales, algo así como un número divino que no pertenece a los números reales pero que es mayor que cualquiera de estos; de igual manera se tiene el infinito negativo (-∞) , el cual es menor que cualquier número real, de allí que la recta real sea denotada por  -∞<x<∞ ó  (-∞,∞) pero para fines prácticos nosotros la denotamos por R

Ahora bien, si queremos visualizar todos los números reales empleamos la recta, pero esta tiene el inconveniente que se extiende sin fin por ambos lados, por lo que observar los elementos próximos a infinito resulta complicado de realizar. Es el mismo fenómeno que ocurre cuando nos encontramos en una calle recta, los objetos cercanos son fáciles de apreciar mientras que aquellos que se encuentran a mayor distancia son más complicados de visualizar, de hecho, llega un momento en el que son imperceptibles.

Lo anterior ocurre sin importar la escala empleada para representar a la recta real. Así que si deseas emplear la recta cómo objeto para visualizar a los números reales necesitas mucho espacio debido a su longitud infinita.

Una pregunta natural es: ¿existe un objeto fácil de manejar y de longitud finita que nos permita representar a los números reales?, o dicho de otra manera, ¿la recta puede transformarse en un objeto de longitud finita? La respuesta es afirmativa y a la transformación encargada de llevarla a cabo se conoce como proyección estereográfica.

Una transformación bastante empleada que transforma una recta en un círculo y que alguna vez hemos utilizado consiste en enrollar la recta como si se tratase de una manguera, hilo o cable y de esta forma obtenemos un círculo; el problema que se presenta radica en que la recta se extiende de manera indefinida a ambos lados, por lo que obtenemos una infinidad de círculos encimados entre sí. Al marcar un punto en la recta y enrollarla, el punto se convierte en un punto del círculo; pero a la inversa no sucede lo mismo ya que si marcamos un punto en el círculo, esta marca se extiende a cada uno de los círculos encimados por lo que al desenrollarlo obtenemos una infinidad de puntos marcados en la recta.

Nos interesa que, por cada punto marcado, también se obtenga un punto después de la transformación y viceversa. La proyección estereográfica es una aplicación que realiza lo anterior. Para construirla consideramos el círculo S^1 de radio 1 centrado en el origen y la recta horizontal y=-1. Tomamos un punto (X,Y) en S^1 y desde el extremo superior (0,1) del círculo trazamos un segmento entre estos dos puntos y lo extendemos hasta que intersecte a la recta horizontal y denotamos a este punto por (x,-1). ¡Listo! Ya tenemos nuestra transformación que envía el punto (X,Y) a x. 

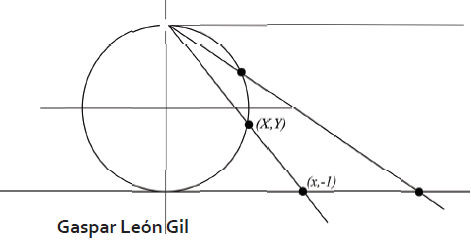
De la figura anterior podemos observar que mientras más próximo sea el punto (X,Y) al extremo (0,1), más alejado se encuentra el punto de intersección de nuestro segmento con la recta y=-1. De hecho cuando (X,Y)=(0,1) tenemos una recta paralela a y=-1, por lo que no existe punto de intersección; esto se interpreta de la siguiente manera: el punto (0,1) se transforma en ∞, pero como este último no pertenece a los números reales, es necesario prescindir del punto (0,1) del círculo S^1 en el dominio de la transformación. Las expresiones matemáticas para la proyección estereográfica P y su inversa P^{-1} son  

Notamos que tanto P como su inversa son diferenciables. A las funciones que son diferenciables con inversa también diferenciable se les conoce como cambio de coordenadas. No es difícil ver que existe un cambio de coordenadas del plano R² a la esfera S² menos el punto (0,0,1).

Así que cuando te soliciten que lleves contigo la recta real, basta transformarla en un círculo menos un punto y llevarla en el bolsillo como si nada, donde los puntos cercanos a (0,1)  representan los puntos cercanos al infinito.

¡Ahora ya puedes visualizar al infinito!, para ello basta mirar el punto (0,1)  del círculo. 

Gaspar León Gil  es Profesor-Investigador en Ingeniería de Petróleos, Universidad del Istmo. 

Dieudonné J. 1981. Elementos de análisis. España: Reverte; Gallego G. 2012. Actualización en geometría: simulación por ordenador. http://slideplayer.es/slide/170706/; Silva-Romo et al. . La enseñanza de la red estereográfica. Educación en Geo ciencias. http://www.ugm.org.mx/publicaciones/geos/pdf/geos02-2/EDUG02-2.pdf