Un sencillo juego que nos divertía cuando niños era el de formar figuras con las sombras de nuestras manos puestas frente a un haz de luz. Dependiendo de los gestos, aparecían siluetas de distintos animales, o al menos eso nos parecía. La destreza consistía en saber cómo poner las manos para que apareciera cierta forma imaginada de antemano. Pensemos ahora una situación similar, pero donde no son nuestras manos lo que proyecta las sombras, sino un objeto desconocido. Lo único que vemos es la forma de la sombra proyectada. ¿Se podrá descubrir de qué objeto se trata?, ¿o al menos, cuál es su forma?
Por ejemplo, si la sombra tiene forma circular, inmediatamente viene a nuestra mente una posible respuesta: una pelota, un balón quizá de futbol. Pero, tras reflexionar unos momentos, nos convencemos que no necesariamente se trata de una pelota o algún otro objeto esférico. Podría ser también, por ejemplo, una lata de conserva orientada en la dirección de la luz, o bien un plato de cocina. Imposible determinar de qué objeto se trata sin mayor información.
Una manera de obtener más información es la de observar las sombras en distintas direcciones. Si el objeto gira, podemos observar cómo cambia la sombra proyectada, lo que nos podría ayudar a determinar la forma del objeto. Podríamos diferenciar, por ejemplo, entre los tres posibles objetos mencionados. La pelota siempre proyectará una sombra circular, independiente de como gire. Si el plato gira en torno a alguno de sus diámetros, su sombra se hará más delgada hasta semejar un segmento de recta. La lata proyectará sombras de distintas formas según su posición: si gira en torno a su eje de simetría la sombra no cambiará, pero sí cambiará si lo hace en otra dirección, hasta proyectar un rectángulo si se encuentra en posición vertical frente a la luz. Podremos decidir entonces cuál de las tres formas mencionadas es la correcta. Esto, si a priori sabemos que se trata de una de estas tres opciones. Si no tenemos ninguna información del tipo de objeto, difícilmente descubriremos de qué se trata, aunque dispongamos de todas las proyecciones posibles.
Una historia de muchas incógnitas.
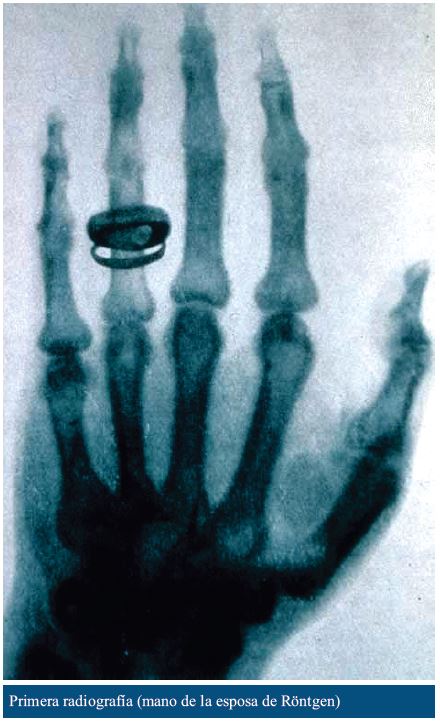
En 1895 el físico alemán Wilhelm Röntgen trabajaba con un tubo de rayos catódicos, cuando notó que una película negra registraba distintas marcas.
Röntgen descubrió que la causante de tales registros era algún tipo de radiación, la cual atravesaba materiales poco densos. La llamó rayos X, por ser de naturaleza desconocida, y estudió sus peculiaridades. Se percató que tales rayos atraviesan el tejido blando, como piel y músculos, mientras que son bastante atenuados por tejido denso, como huesos, y dejan una marca en ciertas películas. Este hecho resultó de gran importancia, dado que permitía ver nuestros huesos (o mejor dicho, ¡su sombra en la película!), sin tener acceso directo a ellos. La primera radiografía conocida fue realizada a la mano de Anna Bertha Röntgen, esposa de Wilhelmn, con anillo incluido. No podemos imaginar la sorpresa de Anna Bertha al ver sus propios huesos, el interior de su mano (se dice que exclamó “¡estoy viendo mi propia muerte!”). Gracias al descubrimiento de los rayos X, Röntgen recibió el primer premio Nobel de Física, en 1901.
Los rayos X resultaron ser la manifestación de una onda electromagnética, como la luz pero de frecuencia mucho mayor. Durante el siglo XX, el uso de ésta y de otros tipos de radiación adquirieron suma importancia para el diagnóstico, e incluso el tratamiento, de diferentes dolencias; son tecnologías de uso común hoy en día. Las radiografías por rayos X tenían sus limitaciones. Una de las principales es la incapacidad para determinar el detalle del tejido blando de un órgano. Si bien las “sombras” de los huesos se pueden ver con claridad en una radiografía, los distintos tipos de tejidos, como músculos o cartílagos, difícilmente se distinguen. Además, una radiografía es una imagen bidimensional, proyección (¡una sombra!), del objeto tridimensional.
Rehaciendo un objeto de sus cortes.
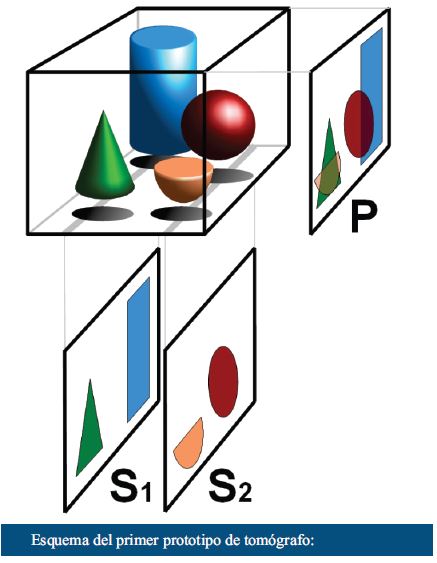
Con la idea de determinar la composición de un objeto tridimensional a partir de las proyecciones de rayos X, varios científicos tuvieron la idea de crear distintas radiografías, cambiando la dirección y el foco de las proyecciones. Se crearían distintos “cortes”, de los cuales se debería reconstruir la forma del objeto. Había surgido la idea básica de la tomografía (del griego “tomos” que significa corte o sección). Pasaron algunos años antes de un estudio sistemático que permitiera aplicaciones prácticas, en particular por la necesidad de una gran capacidad de cómputo para tratar las distintas proyecciones.
En 1966, el físico sudafricano Allan Cormack trabajaba en la Universidad de Cape Town, cuando un hecho fortuito lo llevó a asesorar un día por semana al Departamento de Radiología del principal hospital de la ciudad. Su misión consistía en supervisar el uso del equipo de radioterapia, una actividad algo rutinaria. Cormack fue más allá y se interesó en las limitaciones de la técnica de los rayos X en procedimientos radiológicos. En tales procedimientos se suponía que la radiación atravesaba material homogéneo. Pero en realidad los distintos tejidos tienen distinta densidad, y por tanto la técnica usada presentaba errores en los resultados obtenidos. Cormack pensó que sería muy útil determinar la distribución de densidades del interior del cuerpo humano. Dado que la densidad del tejido es la propiedad que determina la atenuación de los rayos X, se planteó el problema de determinar la densidad de un objeto a partir de la atenuación de los rayos en distintas direcciones.
El problema planteado por Cormack es análogo a nuestro juego de las sombras, sólo que ahora se dispone no sólo de una sombra, sino del grado de atenuación de los rayos, y esto en cada dirección. Es como si observáramos no solamente espacios de sombra y luz, sino sombras en distintas escala de grises, en todas las direcciones posibles. Más allá de la dificultad técnica de determinar el nivel de atenuación de los rayos en todas las direcciones, se abocó al problema de determinar la densidad del objeto desconocido a partir de tal información. Cormack se dio cuenta que esto se trataba de un problema matemático. No encontró bibliografía al respecto, y entonces se dispuso a trabajar en resolver el problema. Consiguió determinar matemáticamente la densidad de objetos en cierta disposición espacial, lo cual fue implementado computacionalmente en varios experimentos. Sus trabajos fueron publicados en 1963 y 1964, pero no obtuvieron un eco inmediato.
En los años siguientes Cormack se enteró de distintos trabajos de otros científicos sobre problemas similares. Sobre todo, se enteró de los trabajos del matemático austriaco Johann Radon, que ya en 1917 había planteado el problema matemático estudiado por Cormack. Radón estudió la transformación que relaciona una función de valores reales en una región dada, con la suma de sus valores a lo largo de distintas líneas rectas (matemáticamente, se trata de una integral de la función sobre la recta dada). Este contexto matemático abstracto corresponde a un modelo muy apropiado para el problema de los rayos y sus atenuaciones. Esta transformación es ahora conocida como Transformada de Radon. En 1917 demostró que tal transformada es invertible, y determinó fórmulas de tal inversión. Esto ya había resuelto parcialmente el problema estudiado (y cuya solución fue re-descubierta) por Cormack, nuestro problema de las sombras en escala de grises.
Cormack también se enteró del trabajo de Godfrey Hounsfield, ingeniero inglés que trabajaba para EMI, Electric and Musical Industries, compañía que también se dedicaba a la edición de discos de música, actividad a la que años después sería su único giro y por la cual quizá nos son conocidas sus siglas. La compañía destinó recursos para construir un prototipo de tomógrafo ideado por Hounsfield en 1967, el que fue utilizado por primera vez en 1972. Como anécdota, se sabe que durante tales años EMI obtuvo grandes éxitos económicos por la venta de discos de varios músicos, muy particularmente de un conocido cuarteto musical inglés: The Beatles. No hay certeza al respecto, pero al parecer tal bonanza económica propició el apoyo financiero de EMI para la construcción del primer tomógrafo. Más allá de las anécdotas, el mérito de Hounsfield fue el de diseñar, de manera independiente a Cormack, algoritmos para reconstruir un objeto a través de sus proyecciones, utilizables en los computadores de esos años.
En el año de 1979, Cormack y Hounsfield recibieron de manera conjunta el premio Nobel de medicina por la invención del método de tomografía computarizada. Para tal fecha, la técnica era usada en más de mil hospitales en el mundo.
Algunas reflexiones.
En esta historia encontramos importantes componentes del trabajo científico. Por supuesto uno es el financiamiento. El apoyo de la empresa EMI al proyecto de Hounsfield fue decisivo para el desarrollo del primer tomógrafo, proyecto que no tenía ninguna seguridad en convertirse en lucrativo. Por otra parte, encontramos la importancia de la colaboración interdisciplinaria: cuando Cormack fue llamado a trabajar en el hospital, probablemente pudo haberse limitado a supervisar el trabajo de los radiólogos. Sin embargo, a partir de necesidades de los médicos identificó un problema científico que pudo ayudar a resolver. Por último, tenemos la importancia de la investigación básica: muy probablemente, en 1917 el matemático Radon no tenía en mente aplicación alguna de su investigación. Su interés radicaba en la importancia matemática de los problemas que estudiaba. Sin embargo, la teoría que desarrolló ha tenido un papel muy importante en el perfeccionamiento del primer prototipo de tomógrafo y en posteriores investigaciones sobre distintas técnicas relacionadas. El mismo Cormack nos relata, en el discurso de aceptación del premio Nobel, que algunos de los problemas en los que él mismo continuó estudiando, tienen en principio, un interés meramente teórico. Estos estudios quizá encuentren una aplicación posteriormente, pero su interés científico actual justifica su existencia, y en sus palabras, eso es “de lo que la ciencia se trata”.
Dr. Alberto Mercado Saucedo es del Departamento de Matemática de la Universidad Técnica Federico Santa María, Valparaíso, Chile